Vai um pouco de física?

Nessa etapa, vamos fazer com que os confetti se comportem como se estivessem sob a ação da gravidade e da velocidade. Além disso, eles não vão ficar colados um no outro, mas sim se "espalhando" pelo canvas.

Para entender as fórmulas explicadas, recomendamos acompanhar juntamente com o código do exemplo prático abaixo.

Mais parâmetros e funções

Antes de explicar os cálculos, iremos para algumas refatorações no código.

Na função confetti, adicionamos mais alguns parâmetros: decay, spread, startVelocity, drift, gravity e angle. A função updateFetti foi movida para um novo arquivo physics.js, juntamente com uma nova função randomPhysics que recebe um objeto com as propriedades do confetti e retorna formatado alguns parâmetros necessários para os cálculos feitos.

Velocidade, gravidade e ângulo

Ao invés de permancecer com um valor fixo, a cada vez que um confetti é atualizado pela updateFetti, um novo valor de x e y são calculados e atribuídos para ele.

No eixo x temos o cosseno do angle2d multiplicado por uma velocidade, somado ao drift. Esse drift é o valor que "freia" o confetti, para ele ter uma explosão incial, mas não em todo seu período de vida. Já no eixo y temos o seno do angle2d multiplicado por uma velocidade, somado ao gravity, que aqui faz o papel de "freiar" como o drift, mas dessa vez no eixo y.

A velocidade e o ângulo demandam algumas características especiais calculadas pela função randomPhysics, que serão explicadas agora.

randomPhysics

Radianos

Logo na primeira linha da função randomPhysics, temos a conversão de graus para radianos tanto da propriedade angle quanto da propriedade spread. Isso facilita os cálculos que precisaremos fazer com eles.

Velocidade

Podemos considerar esse cálculo como dividido em duas partes:

• 1: (fetti.startVelocity * 0.5)
• 2: (Math.random() * fetti.startVelocity)

A segunda parte garante que diferentes confetti tenham velocidades diferentes, fazendo com que os confetti estejam mais espalhados durante e depois do efeito da explosão inicial. Já na primeira parte, é algo mais arbitrários, estamos somando metade da velocidade inicial vezes 0.5, garantindo mais velocidade e mais espalhamento. Se o efeito desejado for diferente, outros valores podem ser usados com base na startVelocity passada.

Angulação

Esse tópico de ângulos é essencial para o confetti, pois ele é o que garante a direção e espalhamento dos confetti. A velocidade também impacta no espalhamento, porém quem mais impacta é o ângulo.

Para entender o cálculo do angle2d, que é -radAngle + ((0.5 * radSpread) - (Math.random() * radSpread)), vamos considerar os seguintes valores:

• angle: 90
• spread: 70

Se consideramos que Math.random() retorna um valor entre 0 e 1, caso o valor retornado seja 0, teremos o seguinte cálculo:

angle2d = -90 + (35 - 70 * 0) = -55

Num círculo, ficaria como na imagem abaixo:

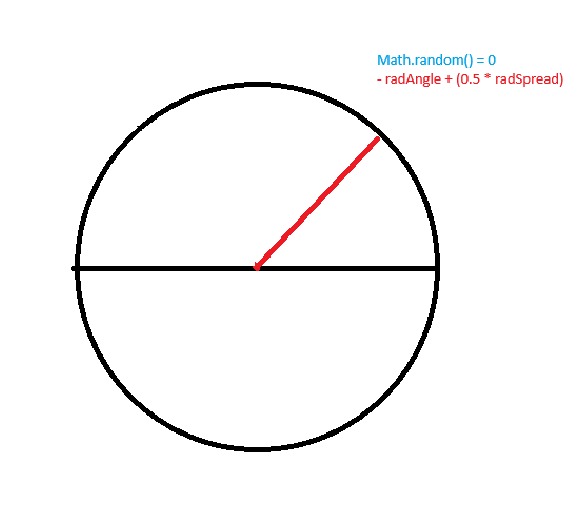
OBS: Deveríamos estar usando radianos, mas para facilitar a visualização, estamos usando graus. Além disso, o grau resultante é negativo, na imagem está sendo representado como positivo para também facilitar a visualização. Existe um motivo para o grau ficar negativo, mas vamos ver isso mais tarde.

Agora, se considerarmos que Math.random() retorna o valor 1, teremos o seguinte cálculo:

angle2d = -90 + (35 - 70 * 1) = -125

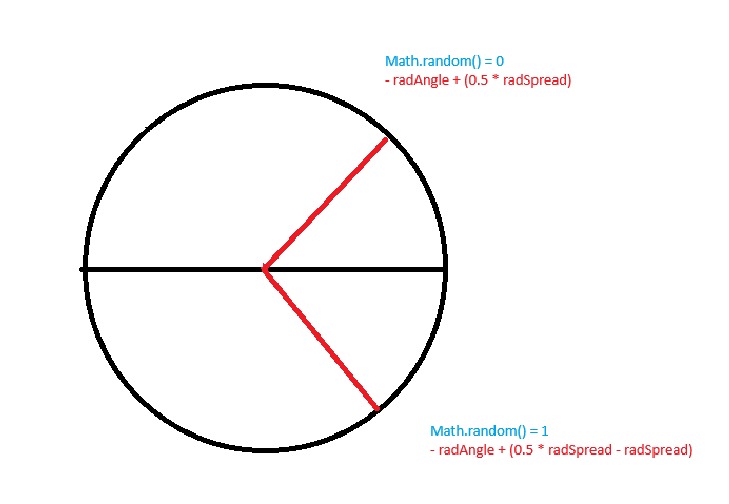
OBS: A posição do ângulo na imagem não está exatamente correta, mas é novamente para facilitar a visualização.

Ou seja, esse cálculo garante que o confetti seja espalhado em um ângulo de 70 graus, com o valor de Math.random() decidindo em que posição entre esses dois pontos representados o confetti vai estar, sendo representado na área abaixo:

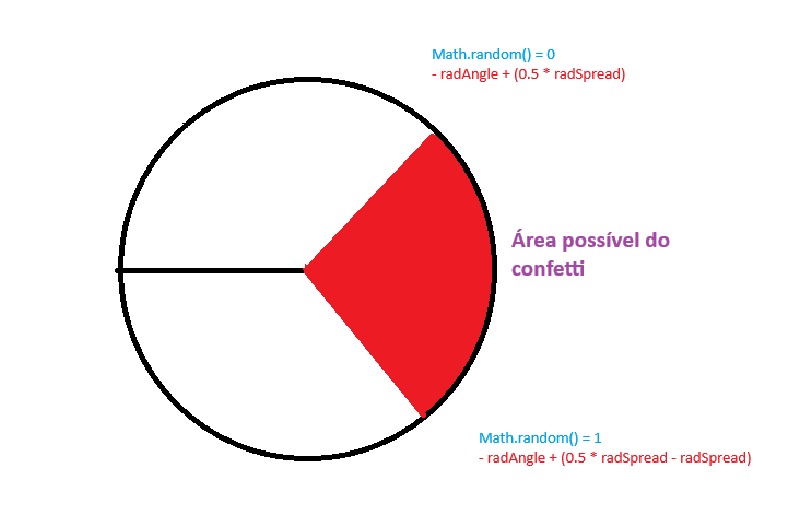
Para que o efeito de espalhamento seja aplicado, precisamos multiplicar o angle2d pela velocidade dentro de updateFetti. Para x usamos o cosseno, já que este é o responsável por nos dar o valor do eixo x de um ângulo. Já para y usamos o seno, pois este é o responsável por nos dar o valor do eixo y de um ângulo. Essas contas definirão a posição do confetti de acordo com o ângulo e spread passados.

Esse ângulo está invertido?

Considerando a posição dos ângulos de acordo com seus valores no cálculo do angle2d, temos o seguinte resultado:

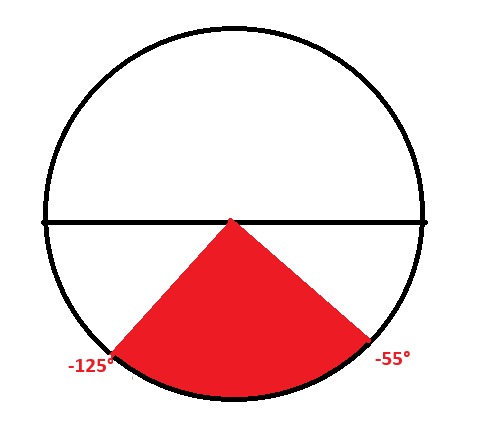
A explicação para o ângulo estar invertido está no canvas. Quanto maior o valor de y, mais para baixo está no canvas. Dentro da updateFetti somamaos novos valores ao y para que o confetti faça o efeito de "cair".

O angle2d está mais relacionado à posição inicial do confetti, logo queremos que esse valor seja negativo para estar o mais para cima possível. Ao fazer o seno de um ângulo negativo, o resultado é negativo.

Tente colocar o angle2d como positivo e veja em que posição os confetti vão "nascer", daí dá para entender melhor o impacto do sinal dos ângulos calculados.

Seno e cosseno, para que tanto cálculo?

Essa definitivamente é a parte mais complicada para recriar o efeito de canhão de confetti. Para entender melhor, tente trocar os valores utilizados, retirar algumas partes e ver como o efeito se comporta. Alguns valores podem parecer meio aleatórios e não fazer nenhum efeito no resultado, mas os manipulando, se percebe sua importância.